trivial improvements on the re-masking strategy of llada

an auto-regressive (AR) language model generates a single token per function call or neural function evaluation (NFE). Language diffusion models are interesting because, in principle, they could generate more tokens per NFE.

llada is, at the time of writing, the largest masked language diffusion model that is competitive with AR models. Its best results are achieved when the number of function calls equals the number of generated tokens. In the paper, the authors report performance as a function of the NFEs. As expected, performance improves when the NFEs are increased to match the generated length of 1024 in the plots below:

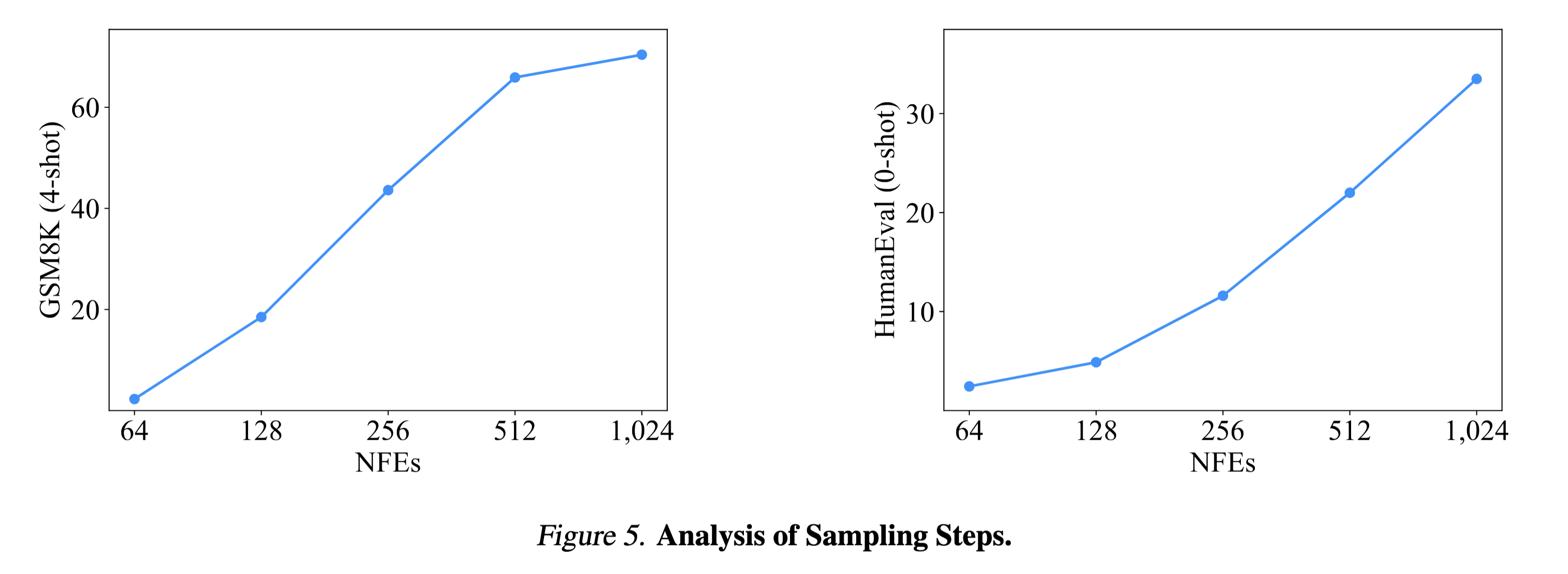
ideally, the plots would have looked more like an early saturating curve, because, in a perfect world, fewer NFEs would be able to match the performance higher NFEs. visually, we would expect:

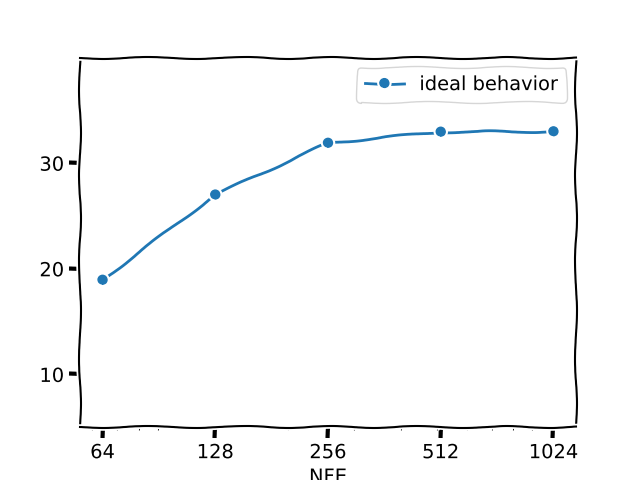
unfortunately the experiments show a curve that does not saturate early. if the NFEs needed to make language diffusion models competitive equals the number of generated tokens, it would defeat the purpose of making a language diffusion model. an AR model would have cost the same and thousands (millions?) of people have already made AR models really good.

re-masking and sampling steps in llada

why can’t we pick fewer NFEs in llada? Two parameters set the token per NFE ratio in llada: the desired number of output tokens gen_length and the number of steps steps used to output them.

llada first begins with a fully masked sequence. At each step, llada unmasks all tokens but only preserves gen_length/steps tokens for the next round. Those tokens are either randomly chosen or selected according to the model confidence. The rest are re-masked before the next step.

if the number of steps is small then at each step a lot of tokens are preserved. Here is what happens at the first step when asking llada-8b-Base to unmask a fully masked sequence:

Input: Hi, I am <|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|><|mdm_mask|> 
Unmasked: Hi, I am 10 years old and I I I........ I I I I....... I I.. I

the unmasked sequence is full of terrible repeated predictions like I and .. The random masking strategy is very likely to preserve those bad tokens. Indeed, here is what happens when trying to generate 32 tokens in 4 steps (this means 8 tokens are kept at each round):

step 0, Keeping: [' I', '.', '.', ' I', '.', '.', '.', '.']
step 1, Keeping: ['\n', '.', ' years', ' am', '.', ' a', '5', '\n'] 
step 2, Keeping: ['\n', '\n', ' .', '.', '\n', '.', ' .', ' I']
step 3, Keeping: ['\n', '\n', '1', '.', '\n', '.', ' student', ' old']

Final output: Hi, I am 15 years old. I am a student..
. 
.. 
. . 
.. I. 
. 
. . I

the model preserved a very large number of . in the first round and struggles to fill in the tokens from there. Clearly, the model struggles to unmask fully masked sequences. Preserving a constant number of tokens at each round seems like a very poor choice. Early rounds should preserve fewer tokens, and later ones should preserve more tokens.

a single line edit to improve performance

instead of picking a uniform random masking strategy, the most basic strategy we can replace it with is a pyramidal one. At the first step 1 token is preserved, 2 at the next step, 3 at the following until steps rounds. This generates steps*(steps-1)/2 tokens meaning that we perform roughly square root(gen_tokens) NFEs. This pyramidal strategy can be implemented in a single line edit in llada’s generate function. At line 103 which sets k to in topk function :

we can replace it by

k = i+1

this is clearly a better choice

Keeping: ['.'] 
Keeping: [' ', '0']
Keeping: [' and', ' to', ' I'] 
Keeping: ['0', ' for', ' I', '.'] 
Keeping: [' been', ' I', ' get', ' years', ' a'] 
Keeping: [' want', ' a', ' to', ' in', ' in', ' Recently'] 
Keeping: ['3', ',', ' have', ' as', '1', ' years', ' old'] 
Keeping: [' want', ' working', ',', 'formatics', ' job', ' teacher', ' know', ' So'] 
Keeping: [' years', '0', ' ', '3', ',', 'Hi', ' I', ' am', ' old'] 

Final output: Hi, I am 30 years old and I have been working as a teacher for 10 years. Recently, I want to get a job in informatics. So, I want to know

had we kept the uniform strategy we would have obtained

Keeping: ['.', '.', ' I', '.'] 
Keeping: [' ', '0', ' I', ' years'] 
Keeping: ['.', ' it', '.', '.'] 
Keeping: [' years', ' for', ' ', ' '] 
Keeping: [' have', ' to', ' ', '2'] 
Keeping: [' lose', ' this', ' lbs', ' is'] 
Keeping: ['3', '2', ' weight', ' carrying'] 
Keeping: ['5', ' been', ' want', ' currently'] 
Keeping: [' My', '1', ' weight', ' old'] 

Final output: Hi, I am 30 years old. I have been carrying this weight for 2 years.. I want to lose it. My weight is currently 12.5 lbs.

notice that under the uniform strategy, the model commits to too many . at the beginning and cannot recover from the two consecutive . chosen.

formally defined, the pyramidal strategy says: if we want to generate gen_length tokens, we can choose steps = int((2*gen_length)**0.5) + 1 and keep k=i+1 tokens at each step i. if we can afford to take more steps we can dilate the pyramid:

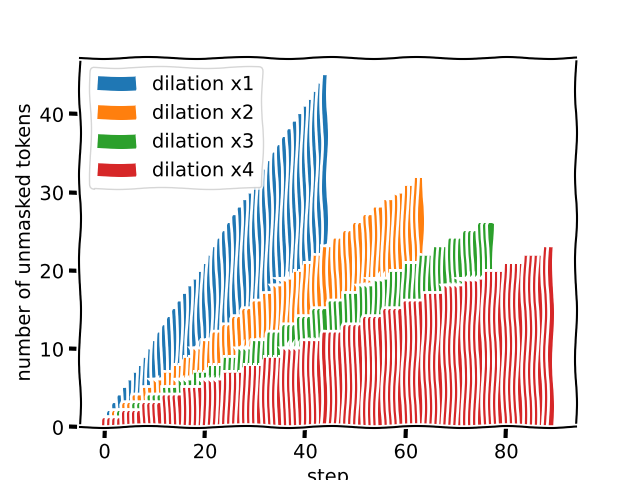
in equation form, if we wish to dilate the pyramid by a factor and generate gen_length tokens, we must take steps = int(factor*(1 + 8 * gen_length/factor)**0.5/2) and, at each step, pick k = i//factor+1 tokens. the modified generate function is provided at the end of this post.

eval results with the pyramidal strategy on humaneval

i found the cheaper eval to run was the HumanEval code generation benchmark. here is what is obtained with the pyramidal strategy and low-confidence re-masking:

the basic pyramidal strategy is much closer to the expected ideal behavior and easily outperforms the llada strategy.

llada does not feel like a ‘real’ diffusion model

the pyramidal sampling strategy is too simple, the authors of llada, i’m sure, must have explored similar things. these trivial improvements are not the interesting research direction. the better question to investigate is why there aren’t large language diffusion models designed to re-mask previously unmasked tokens. A large language diffusion model that commits too early to tokens and doesn’t reset its early decisions is missing the essence of a diffusion model.

the modified generate function:

def generate(model, prompt, factor=1, gen_length=128, block_length=128, temperature=0.,
             cfg_scale=0., remasking='low_confidence', mask_id=126336):

    x = torch.full((1, prompt.shape[1] + gen_length), mask_id, dtype=torch.long).to(model.device)
    x[:, :prompt.shape[1]] = prompt.clone()

    prompt_index = (x != mask_id)

    assert gen_length % block_length == 0
    num_blocks = gen_length // block_length
    
    steps = int(factor*(1 + 8 * gen_length/factor)**0.5/2)

    for num_block in range(num_blocks):
        block_mask_index = (x[:, prompt.shape[1] + num_block * block_length: prompt.shape[1] + (num_block + 1) * block_length:] == mask_id)
        for i in range(steps):
            if i > gen_length:
                break
            mask_index = (x == mask_id)
            if cfg_scale > 0.:
                un_x = x.clone()
                un_x[prompt_index] = mask_id
                x_ = torch.cat([x, un_x], dim=0)
                logits = model(x_).logits
                logits, un_logits = torch.chunk(logits, 2, dim=0)
                logits = un_logits + (cfg_scale + 1) * (logits - un_logits)
            else:
                logits = model(x).logits

            logits_with_noise = add_gumbel_noise(logits, temperature=temperature)
            x0 = torch.argmax(logits_with_noise, dim=-1) # b, l

            if remasking == 'low_confidence':
                p = F.softmax(logits, dim=-1)
                x0_p = torch.squeeze(
                    torch.gather(p, dim=-1, index=torch.unsqueeze(x0, -1)), -1) # b, l
            elif remasking == 'random':
                x0_p = torch.rand((x0.shape[0], x0.shape[1]), device=x0.device)
            else:
                raise NotImplementedError(remasking)

            x0_p[:, prompt.shape[1] + (num_block + 1) * block_length:] = -np.inf

            x0 = torch.where(mask_index, x0, x)
            confidence = torch.where(mask_index, x0_p, -np.inf)

            transfer_index = torch.zeros_like(x0, dtype=torch.bool, device=x0.device)
            for j in range(confidence.shape[0]):
                _, select_index = torch.topk(confidence[j], k=i//factor+1)
                transfer_index[j, select_index] = True
            x[transfer_index] = x0[transfer_index]

    return x